「時間は一方向にしか流れない」

人類史上　最重要方程式ベスト10 その9

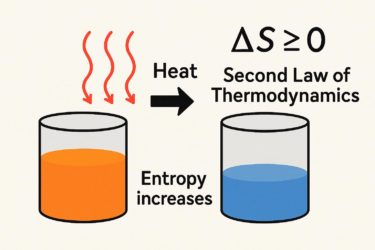
熱力学第2法則はエントロピー増大を通して不可逆性を示す。

熱力学第2法則とは？
「エネルギーは使えば使うほど“使いにくくなる”法則」

1. そもそも「エントロピー（S）」ってなに？
エントロピーとは、「エネルギーの散らばり具合」や「無秩序さ」のこと。
整っている状態 → エントロピーが低い
ごちゃごちゃした状態 → エントロピーが高い
たとえば、インクを水にたらしたときを思い出してみてください。
最初は、インクは一点に集中（エントロピーが小さい）
時間が経つと、全体に広がっていく（エントロピーが大きくなる）このように、エネルギーや物質は、自然に“広がる方向”に向かうんです。

2. 第二法則の代表的な式
ΔS ≥ 0
これは閉じた系（＝外部とやりとりのない世界）で、
エントロピーは減らない（増えるか、同じか）
という意味です。
さらにもう一歩進むと、カルノーサイクルなどから導かれる、次のような表現もあります。
dS = δQ / T
dS：エントロピーの微小変化量
δQ：吸収した熱量
T：絶対温度（ケルビン）
これは可逆過程（理想的な熱のやりとり）に限った式ですが、ポイントは：
同じ熱量でも、温度が低い場所に熱を与える方が、エントロピーはより増える

3. 何がそんなにすごいの？
（1）時間に「向き」があると証明した
ニュートン力学や量子力学の多くの方程式は時間に対して対称（時間を逆にしても式が成り立つ）なのに対し、
熱力学第二法則だけは、「時間は必ず未来に進む」という非対称性を持ちます。
これは「時間の矢（Arrow of Time）」と呼ばれ、物理学において特別な位置を占めています。

（2）すべてのエネルギー変換に“限界”を与える
たとえば、100℃のお湯の熱エネルギーをすべて電気に変えることはできません。
その理由は、
熱エネルギーの一部は、必ずエントロピーを増やす形で失われるから。
これにより、永久機関の存在は不可能だと論理的にわかります。

（3）宇宙の未来とつながる
エントロピーが増え続けると、宇宙全体は最終的に
熱が均一に広がりきった、変化のない「死んだ状態」
に至ると予想されています。これがいわゆる「熱的死（heat death）」です。
つまり、この法則はコーヒーが冷めることから宇宙の終焉までを支配しているんです。

まとめ：第二法則の「深さ」
視点 影響
日常 部屋が散らかる、アイスが溶ける
科学技術 エンジン効率の限界、冷蔵庫の設計
哲学 時間はなぜ戻らないのか？
宇宙論 宇宙はどう終わるのか？
この「当たり前のような変化」に隠された法則が、式一つ（ΔS ≥ 0）で貫かれていることに、自然科学の美しさがあります。

ブラック＝ショールズ方程式

人類史上　最重要方程式ベスト10 その8

ブラック＝ショールズ方程式（Black-Scholes equation）は、株やオプションなどの金融商品の「価格の未来」を予測するための数式です。

でも、中学生向けにするには、まず「オプションって何？」というところから入りましょう。

【ステップ1：オプションってなに？】

たとえば、あなたが「1か月後に100円でチョコを買える券」を持っているとします。
1か月後、チョコの値段が120円になっていたら…あなたは券を使ってお得に買えます。
逆に、チョコの値段が80円だったら…その券は使わない方がいいですよね。
この「未来の価格によって得をするかもしれない券」が、金融の世界で言う「オプション（権利）」です。

【ステップ2：オプションの価値をどう決める？】

問題はこの券がいくらの価値なのか、です。
今のチョコの値段
どれくらい価格が変動しそうか（＝「変動性」）
期限までどのくらい時間があるか
この3つが分かれば、その「券（オプション）」の今の値段がだいたい分かる…それを計算するのがブラック＝ショールズ方程式です。

【3. 何をしている式なのか？】
この式は、オプションの価格が「時間」と「株価の変化」からどのように変わるかを数式で捉えたものです。
左辺：時間や株価の影響でオプション価格がどう変わるかを表現。
右辺：金利が価格に与える影響。
この式を満たすような V(S,t) を求めることで、「正当なオプション価格」がわかるというわけです。

【4. 導出の考え方：確率 × 微分】
ブラック＝ショールズ方程式は以下のアイデアに基づいています：
株価は確率的（ランダム）に動く（ブラウン運動に従う）
株とオプションを組み合わせて「リスクのないポートフォリオ」を作る
そのポートフォリオは確実に一定の利子で増えると仮定
その理論から、オプション価格に満たされるべき条件（微分方程式）が導かれる

【5. ブラック＝ショールズモデルの意義】
1973年にフィッシャー・ブラックとマイロン・ショールズがこのモデルを発表（のちにロバート・マートンが拡張）。1997年にはマイロン・ショールズとロバート・マートンがノーベル経済学賞を受賞しました（ブラックはすでに逝去していたため対象外）。
この方程式は、デリバティブ（金融派生商品）市場の爆発的な発展を支えた「金融工学の革命的発明」と評価されています。

【6. 現実との違い】
実際の市場では：
ボラティリティは一定ではない
株価は飛び跳ねる（ジャンプ）こともある
取引コストや税金も存在する
そのため、ブラック＝ショールズ方程式は「理想的な仮定のもとでの近似モデル」とされています。

面白い事考えつくなあ。思わず買いそうになった。

トミーカイラ創始者の富田義一さんの京都のお店を訪問しました。

前にお会いしたのは、下手したら10年近く前の事になってしまったかもしれませんが、藤もっちゃんが来るならとお店に顔を出してくれました。

海外からのお客さんが本当に多いのだそうですが、Tommykaira ZZが世界的に著名になったのは、PlayStationのグランツーリスモ1、2の影響なのだそうです。むべなるかな。

世界から尊敬を集めるモータースポーツ界のレジェンドはもう80歳。

実は今年は大きな発表もあるそうです。楽しみです。

「原子は波でできている」

人類史上　最重要方程式ベスト10 その7

シュレーディンガー方程式が電子のふるまいを波動関数で表現す

シュレーディンガーの方程式とは？

簡単にいうと、
「目に見えない小さな世界（原子や電子など）が、どのように動いているのかを予想するための方程式」です。

■ なぜ必要なの？
ふつうの大きさの世界（たとえば車やボール）では、「ニュートンの法則」で動きが予想できます。
でも、電子や原子のようなすごく小さな粒では、その動きが“はっきりとは決められない”という不思議な性質があります。

■ 例えてみよう
たとえば、電子はボールのように「ここにある！」とはっきり言えません。
むしろ「このへんにある可能性が高い」としか言えないのです。
そこで登場するのが「シュレーディンガーの方程式」。

■ じゃあ何をするの？
この方程式を使うと、
電子がどこにいそうか（確率）
どういうふうに動いていそうか
原子のエネルギーの大きさ
などがわかります。

■ 波？ 粒？ どっち？
実は電子や光は、「粒（つぶ）」でもあり「波」でもあるという性質があります。
これを「波動性と粒子性の両立」といいます。
シュレーディンガーの方程式は、この「波のような性質」を使って、小さな世界のふるまいを予測しているのです。

■ 猫の話とどうつながる？
シュレーディンガーの猫の話は聞いた事がありませんか？
物理学者エルヴィン・シュレーディンガーが1935年に考えました。

内容は
【思考実験の設定】

密閉された箱の中に
1匹の猫
放射性物質（たまに崩壊する）
放射性物質が崩壊したら毒ガスが出る装置
が入っています。

放射性物質は、
50%の確率で1時間以内に崩壊して毒ガスが出て猫が死ぬ
50%の確率で崩壊せず猫は生きている

ここでの問題
外から箱の中が見えないとき、「猫は生きているか、死んでいるか？」
量子力学的には、崩壊した状態と崩壊していない状態が重ね合わさっていると考えます。

つまり…箱を開けるまで、猫は
「生きている状態」と「死んでいる状態」が両方重なっている」＝「生きていて、かつ死んでいる」
という、ふつうの世界では信じられない状態にあるのです。

猫の話は「量子の世界」と「マクロな（大きな）世界」との境界問題をあぶり出すための皮肉交じりの実験です。

放射性物質の崩壊は、シュレーディンガー方程式で説明される量子のふるまいです。

でも、それが猫の「生死」という私たちの世界にある明確な事象とつながってしまうと、理論上、猫の生死も「確率の重ね合わせ（生きてる＋死んでる）」であるはずという結論になります。

■ 問題提起：観測によって現実が決まる？
量子力学では「観測（観ること）」によって、波のような状態が一つの現実に“収束”する（波束の収縮）」とされます。
箱を開けるまでは、猫は生きても死んでもいる
箱を開けた瞬間に、生きているか死んでいるかが決まる
→ これがシュレーディンガー方程式が内包する哲学的な問題であり、「量子の奇妙さは本当に現実にまで及ぶのか？」という問いかけになるのです。

■ まとめ
シュレーディンガーの方程式は「小さな粒のふるまいを予想する式」
電子は“波のように”ふるまう
どこにいそうかを確率で予測する
現代の量子力学の中心的な考え方