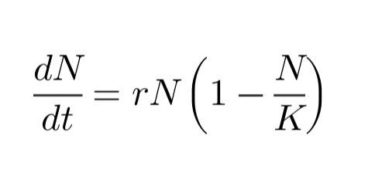「重力って、空間がゆがむことだったんだ！」

人類史上　最重要方程式ベスト10 その5

アインシュタインが教えてくれた、宇宙の新しいルール

重力場方程式（一般相対性理論）

1．「重力」ってなに？

みんながよく知ってる「重力」は、リンゴが木から落ちる力。ニュートンが発見しました。
でもアインシュタインは「重力は“引っぱる力”じゃなくて、“空間がゆがんでるから落ちる”んだよ」と言ったんです。

2．トランポリンを想像してみて！

大きなトランポリンの真ん中に重たいボウリングの玉を置くと、その周りがくぼみますよね？
そこに小さなボールを転がすと、くぼみに引き寄せられていきます。

• トランポリン＝宇宙（時空）
• ボウリングの玉＝太陽や地球などの重たい星
• くぼみ＝空間のゆがみ
• 小さなボール＝月や人工衛星などの軽い物体

つまり、重力とは「空間のくぼみ＝ゆがみ」に物が落ちていくことなんです。

3．時間もゆがむ？

アインシュタインは「時間も空間と一緒にゆがむ」と考えました。
たとえば、重たい星の近くでは、時間がゆっくり進むんです。
これを「時間の遅れ（重力による時間の遅れ）」と呼びます。
実際に、地球の上空にあるGPS衛星ではこの効果を計算に入れて調整しないと、位置情報がずれてしまうほど。

4．アインシュタインのスゴいところ

ニュートンでは説明できなかったこと（たとえば水星の動きのズレ）を、この理論でピタリと説明しました。
また、ブラックホールや重力レンズ（光さえ曲げてしまう重力）なども、一般相対性理論が予言していたことが、後から観測で確かめられました。

5．まとめ：空間も時間も「柔らかい」

重い物があると空間がゆがむ
　　空間がゆがむと、物体はその方向に動く
時間もいっしょにゆがむ

宇宙はただの「空っぽの箱」じゃない。柔らかくて、重さに反応する「布」のようなものなんだ！

6．図で説明するとこう！

【図のイメージ：トランポリンにボールがのって、その周りがへこむ】
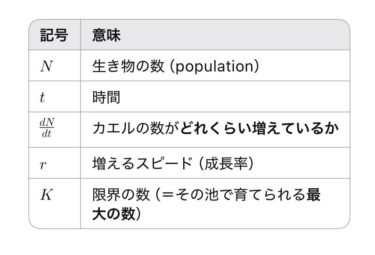
ボール＝物質（T）
へこみ＝時空のゆがみ（G）

つまりこの式はこう言ってます：

「物があるところに、空間と時間のゆがみができる」
→ それが“重力”として感じられる！

7．なんでこの式がすごいの？

ニュートンの重力は「距離と質量で決まる引っぱる力」だった。
アインシュタインは「空間と時間そのものが曲がる」と考えた。
しかも、光さえもそのゆがみに沿って曲がるという。

8．この方程式が予言したこと（すべて現実に観測された）

　水星の軌道のズレ（ニュートン理論では説明不能）
　ブラックホールの存在
光が曲がる（重力レンズ）
重力波（2015年にLIGOで観測）

まとめ：一言でいうと？

「物質があると、時空がゆがみ、そのゆがみの中を物が動く」
→ それが「重力」だった！

「水も空気もこの数式」

人類史上　最重要方程式ベスト10 その4

ナビエ–ストークス方程式は流体の動きを支配する力のバランス式

ナビエ–ストークス方程式（Navier–Stokes equation）は、一言で言えば、
「空気や水がどう動くかを決めるルール」
です。

飛行機　空気の流れから「揚力（うきあがる力）」を計算
医学　血液の流れ（心臓のポンプや血管）
天気予報　雲や風の流れをシミュレーション
宇宙　惑星の大気、星の形成のしくみ
などなどを計算します。

■ たとえば空気や水は「動く」もの

• 水をコップに注ぐと流れます。
• 空を風が吹きます。
• プールで泳ぐと水が押し返してきます。

こうした流れるもの（流体）の動きを計算するための「数式のルール」が、ナビエ–ストークス方程式です。

■ 何が決まるの？

この方程式を使うと、次のようなことがわかります

どんなこと？

流れるスピード　水道の水が速くなる場所・遅くなる場所
流れる方向　風がどっちに曲がるか（台風の進路）
押し返す力　飛行機の翼がどう lift（浮力）を受けるか

式の要素は

速度　どれくらい速く動いてる？　水や風の速さと方向
圧力　どれくらい押されてる？　指で押すと感じる力
粘性　どれくらい「ねばる」？　水はサラサラ、ハチミツはねばねば
密度　どれくらい中身がつまってる？　空気と水で違う

ナビエ–ストークス方程式は、「水や空気がどう流れるかの地図」
速さ・向き・圧力・ねばりけの関係を数式にしている
飛行機、台風、血液、宇宙の中まで、全部この方程式が関係してる！

■ ナビエ–ストークス方程式の重要性

すべての流体の動きの基礎式

実はまだ数学的には未解決の部分があり、「粘性ありの三次元流体で解が常に存在するか？」はミレニアム懸賞問題（7大難問）のひとつです。
「ナビエ–ストークス方程式に対して、3次元空間において、時間的に滑らか（無限大の発散が起きない）な解が常に存在するか？」

なぜ難しいの？
現実の水や空気は乱流（turbulence）を起こすことがあり、そのときに数学的な「爆発」（無限大）が起こる可能性がある。でも「爆発せずに常に解が存在する」ことを数学的に証明できていない。

何がかかってるの？
これは「流体力学の完全な理解」に直結する。
天気予報、航空力学、エネルギー、医学などの基礎がこれに関わる。

「増えるけど、限界がある」

人類史上　最重要方程式ベスト10 その3

ロジスティック方程式は生物や現象の成長と抑制をS字カーブで描く。

ロジスティック方程式（logistic equation）は、「増えるけど、限界がある」という自然界の現象をとてもよく表す数式です。中学生でもわかるように、やさしく説明します。

■ ロジスティック方程式ってなに？

意味をざっくりいうと…
「最初はどんどん増えるけど、そのうち限界に近づくとゆっくりになって、やがて止まる」という生き物や人の数の変化を表す式です。

分野　使い方の例
生物学　生き物の数の変化（カエル、バクテリア、人口など）
医学　ウイルス感染の広がり（最初は急、あとから鈍化）
経済学　製品の売れ方（発売直後→急増→頭打ち）
SNS フォロワー数やバズの広がり方もこれに近い！

■ 具体例で考えてみよう！

たとえば、ある池にカエルが住んでいるとします。
最初はカエルが少ない → エサも住む場所もたっぷり → どんどん増える
カエルが増えてくる → エサが足りなくなる → 増え方がゆるやかになる
限界に達する → 増えるのが止まる
この「増えるけど止まる」という自然な流れを数学で表したのがロジスティック方程式です。

■ まとめ（中学生向け）

ロジスティック方程式は「増えすぎない増え方」をあらわす
最初は増える、でもだんだん限界に近づいて止まる
生き物、感染症、SNS、売上など、いろんな現象に使える！